Significant advancements in deep neural networks have led to developments in wireless communication. However, these deep learning-based methods require extensive training data, which is impractical to collect in real-world environments. For example, training beam alignment algorithms requires around 100K channel measurements for a typical macrocell sector. Existing methods can perform suboptimally if only a limited number of data samples are available at specific locations. Therefore, we suggest a channel data synthesizing method using a conditional diffusion model, which captures the distribution of the site-specific channel and boosts the dataset.
Problem setup
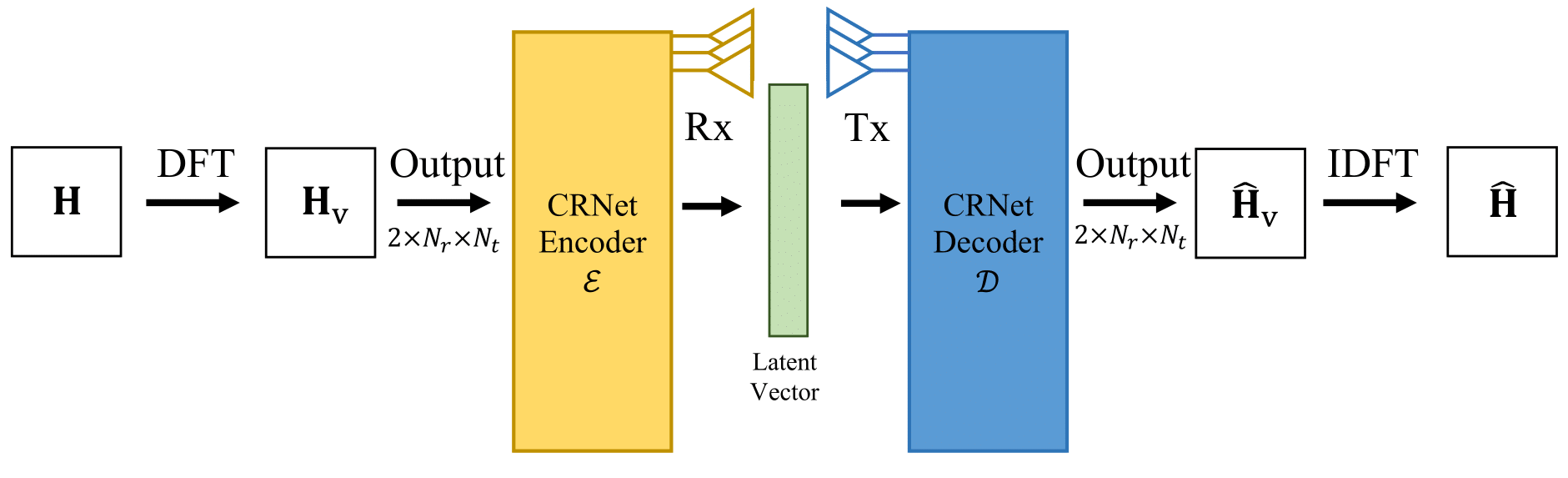
We focus on the narrowband MIMO system, where the channel matrix is \(\mathbf{H}\) at position \(\mathbf{x}\). We utilize the key insight that the beamspace representation of mmWave MIMO channels exhibits high spatial correlation, enabling the diffusion model to capture the distribution effectively. Therefore, we consider the beamspace representation using DFT, defined as \(\mathbf{H}_\mathrm{v} = {\mathbf{A}_r}^{H} \mathbf{H} \mathbf{A}_t\) where \(\mathbf{A}_t\) and \(\mathbf{A}_r\) are unitary DFT matrices.
The primary objective of this work is twofold: (a) to develop a model that estimates the channel matrix \(\mathbf{H}_\mathrm{v}\) from the user’s position \(\mathbf{x}\) by implicitly determining the relevant parameters, and (b) to use this model to boost the dataset for training downstream task models that require a set of channel matrices.
We have \(N_\mathrm{train}\) pairs of position-channel dataset, labeled as \((\mathbf{x}_{\mathrm{train},i}, \mathbf{H}_{\mathrm{v,train},i})\), where \(i \in \{1, \ldots, N_\mathrm{train}\}\). Our goal is to expand this dataset by randomly selecting \(N_\mathrm{aug}\) positions \(\mathbf{x}_{\mathrm{aug},i}\) for \(i \in \{1, \ldots, N_\mathrm{aug}\}\), and generating \(N_\mathrm{aug}\) estimated channels \(\widetilde{\mathbf{H}}_{\mathrm{v,aug},i}\), where \(i \in \{1, \ldots, N_\mathrm{aug}\}\). This allows us to create an augmented dataset with \(N_\mathrm{train} + N_\mathrm{aug}\) pairs of position and channel data.
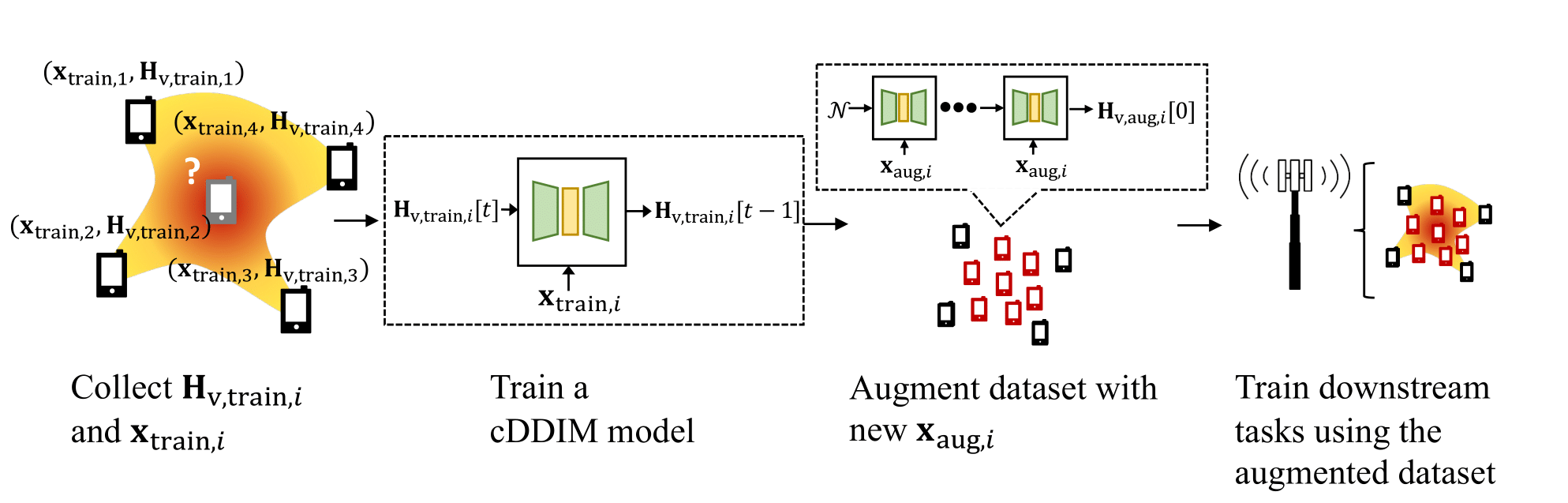
Diffusion Model
Suppose we want to generate channels according to the conditional channel distribution \(p(\mathbf{H}_\mathrm{v}|\mathbf{x})\) for a given position \(\mathbf{x}\). If we know the distribution \(p(\mathbf{H}_\mathrm{v}|\mathbf{x})\), it is ideal. What if we are not given the distribution itself but a collection of measurement channels \(\{(\mathbf{x}_{\mathrm{train},i}, \mathbf{H}_{\mathrm{v,train},i})\}_{i=1}^{N_\mathrm{train}}\)?
To generate samples that follow a specific distribution \(p(\mathbf{H}_\mathrm{v}|\mathbf{x})\), we utilize the concept of a score function, which is defined as \(\nabla_{\mathbf{H}_\mathrm{v}|\mathbf{x}} \log p(\mathbf{H}_\mathrm{v}|\mathbf{x})\). This score function is used in conjunction with Langevin dynamics to generate the desired samples as follows: Let \(\mathbf{N}_{ij} [t] \sim \mathcal{N}(0, 1) \text{ for } i = 1, \ldots, N_t, j = 1, \ldots, N_r\) and for \(1 \le t \le T\), \(\mathbf{H}_\mathrm{v}[t-1] = \mathbf{H}_\mathrm{v}[t]+\frac{\sigma^2}{2} \nabla_{\mathbf{H}_\mathrm{v}[t]|\mathbf{x}} \log p\left(\mathbf{H}_\mathrm{v}[t]|\mathbf{x}\right)+ \sigma \mathbf{N}[t]\).
To optimize the parameterized DNN, denoted as \(\mathbf{S}(\mathbf{H}_{\mathrm{v}}|\mathbf{x}; \mathbf{\Theta})\), we aim to minimize the explicit score matching loss function
\[\mathcal{L}_{\mathrm{exp}}(\mathbf{H}_{\mathrm{v}}|\mathbf{x}; \mathbf{\Theta}) = \frac{1}{2} \mathbb{E}_{\mathbf{H}_{\mathrm{v}}} \left[ \left| \mathbf{S}(\mathbf{H}_{\mathrm{v}}|\mathbf{x}; \mathbf{\Theta}) - \nabla_{\mathbf{H}_{\mathrm{v}}|\mathbf{x}} \log p(\mathbf{H}_{\mathrm{v}}|\mathbf{x}) \right|^2 \right]\]to approximate the score function. However, since the underlying distribution is unknown, we cannot calculate this exactly. Instead, we use denoising score matching techniques to learn the score function from samples.
Minimizing the denoising score matching loss function below
\[\mathcal{L}_{\mathrm{den}}(\widetilde{\mathbf{H}}_{\mathrm{v}}|\mathbf{H}_{\mathrm{v}}, \mathbf{x}; \mathbf{\Theta}) = \frac{1}{2} \mathbb{E}_{\mathbf{N} \sim \mathcal{N}(0, \mathbf{I})} \left[ \frac{1}{\sigma} \left| \widetilde{\mathbf{S}}(\widetilde{\mathbf{H}}_{\mathrm{v}}|\mathbf{x}; \mathbf{\Theta}) - \mathbf{N} \right|^2 \right]\]is equivalent to minimizing the above explicit score matching loss function, and this does not require knowing the underlying distribution. We can train the neural network by predicting the added Gaussian noise in the denoising process.
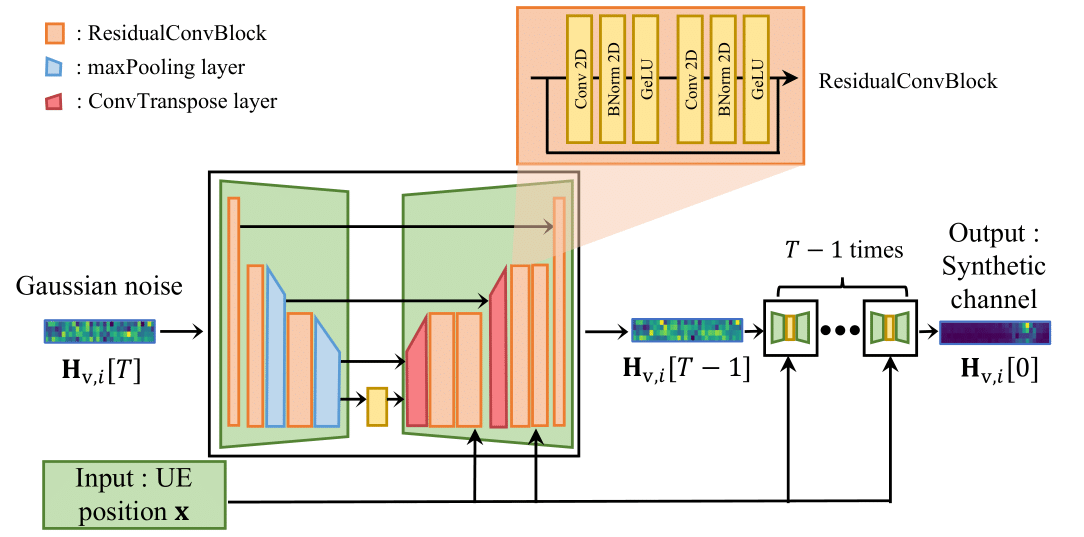
We use conditional Diffusion Denoising Implicit Model (cDDIM) by denoising for \(T = 256\) iterations and providing the UE position \(\mathbf{x}\) as a conditional input to the model.
Visualization of the channel
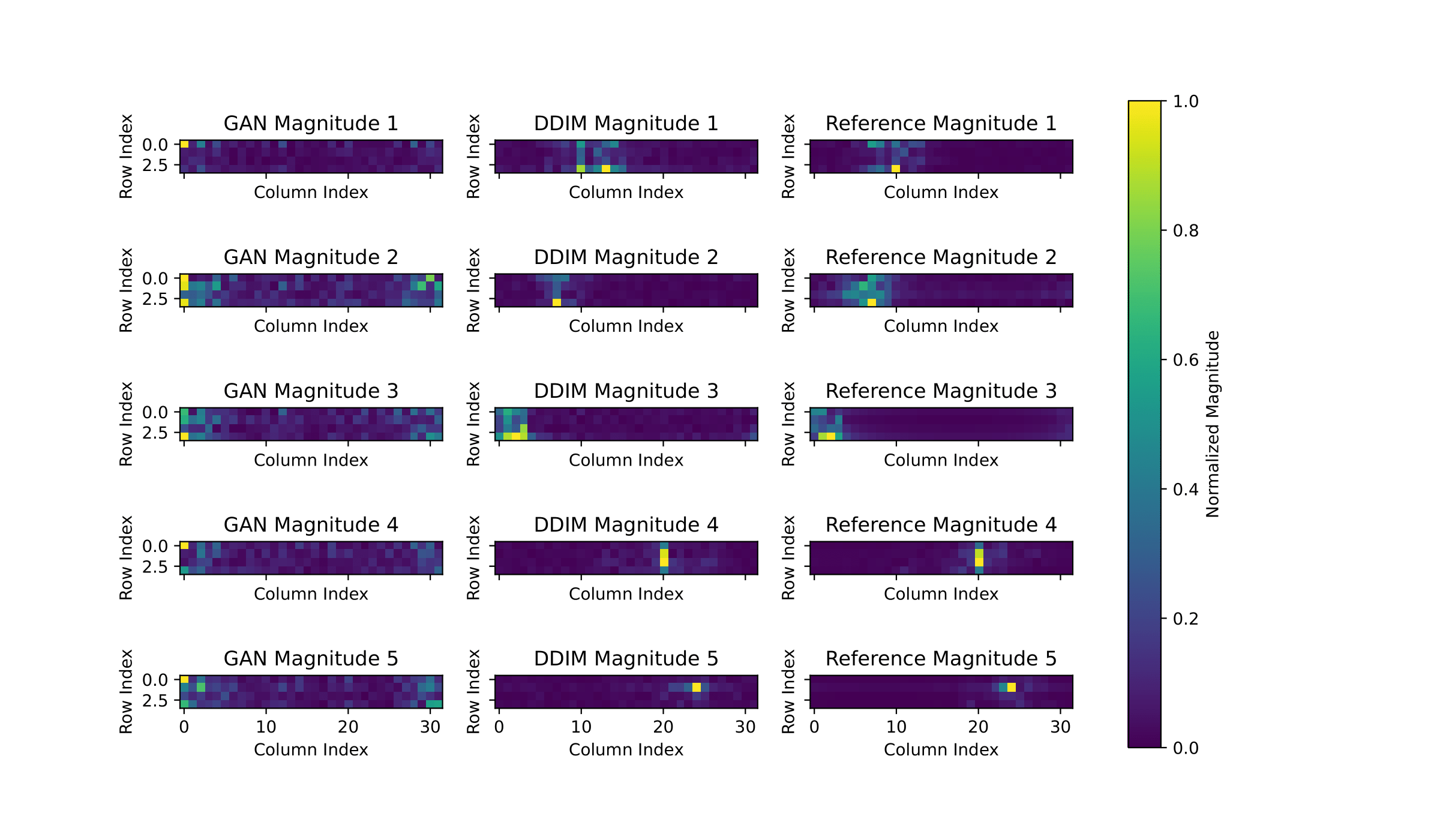
We compare channels generated by cGAN, cDDIM, and the reference channels. The visualization highlights how each method predicts the peak BS index in the LOS path. cGAN produces channels that lack diversity and consistently place the peak at similar coordinates in the synthetic channels. In contrast, the middle column, the cDDIM-based generated channel, demonstrates that the BS index of the peak in the beamspace domain is always similar to that of the reference channel matrix. This indicates that cDDIM can make accurate estimates given the UE coordinates, resulting in a dataset with correct predictions.
Evaluation of the dataset
NMSE is not an effective metric for evaluating the realism of generated channels due to phase shifts. For instance, even if the estimated channel is perfect with only a phase difference, \(\widetilde{\mathbf{H}}_\mathrm{v} = e^{j\theta}\mathbf{H}_\mathrm{v}\), when \(\theta = \pi\), \(\mathrm{NMSE}=\mathbb{E}\left\{\frac{\left\|\widetilde{\mathbf{H}}_{\mathrm{v}}-\mathbf{H}_{\mathrm{v}}\right\|_2^2}{\left\|\widetilde{\mathbf{H}}_{\mathrm{v}}\right\|_2^2}\right\} = 4.\) Therefore, evaluating the performance of downstream tasks is a more viable. We choose three different deep-learning based solutions for the wireless communication problem to evaluate the augmented dataset. In this post, we will introduce two of them.
Downstream task 1 : Channel Compression
In this task, we focus on improving CSI feedback in MIMO systems. Specifically, we aim to evaluate the NMSE of reconstructed Downlink CSI using different dataset augmentation methods. The goal is to minimize the NMSE between the original and reconstructed CSI with minimal training data. We utilize CRNet [2] as the backbone method for channel compression and reconstruction, with detailed descriptions omitted for brevity.
Result of Downstream task 1
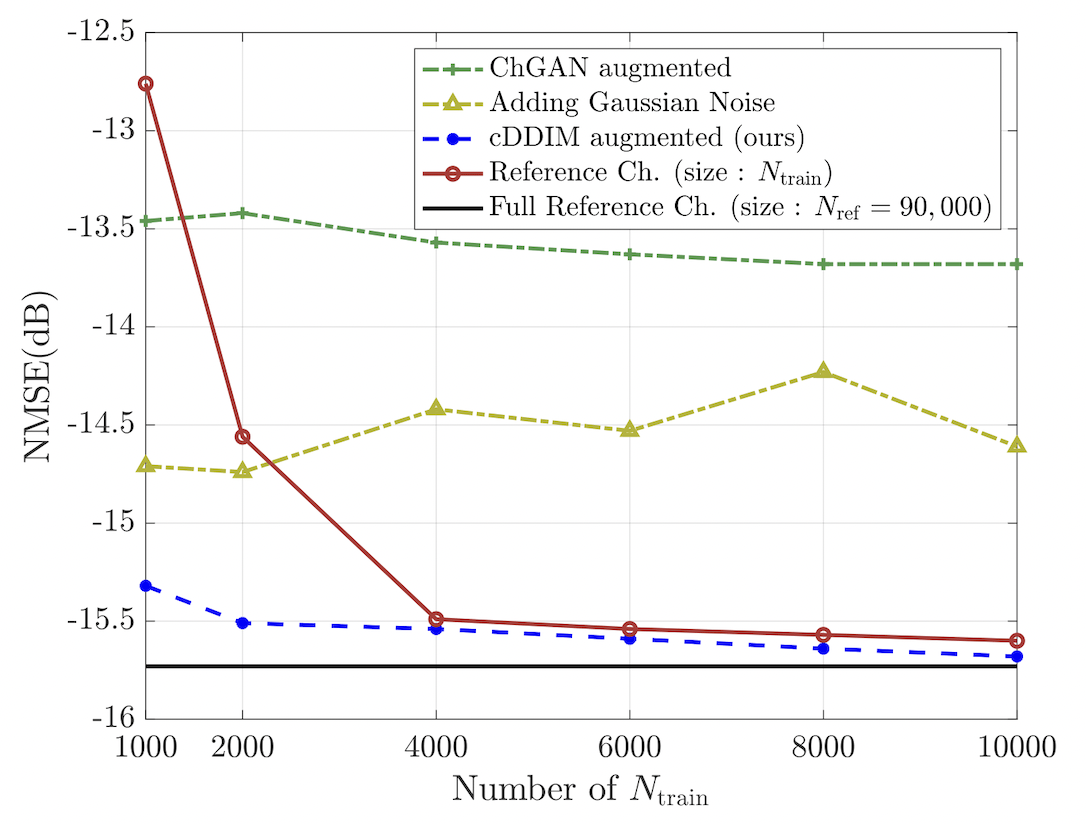
The black solid line represents the NMSE when CRNet is trained with 90,000 reference samples, serving as the lower bound of NMSE performance. The red line with o markers shows the NMSE when CRNet is trained with varying numbers of reference samples. For 1,000 reference channels, the NMSE sharply deteriorates by 3 dB compared to the black line. However, augmenting the dataset with cDDIM to 90,000 samples (blue line with o markers) keeps the NMSE within 1 dB of the black line, even starting with only 1% of the total dataset. This demonstrates that diffusion-based augmentation can maintain low NMSE with a small training set. Other methods, such as adding Gaussian noise (yellow line with triangular markers) and ChannelGAN-based augmentation (green line with + markers), fail to achieve distortion below -15dB.
Downstream task 2 : Site-Specific Beamforming
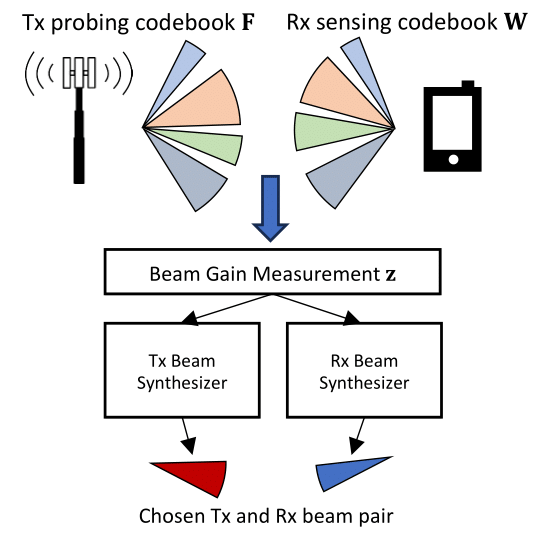
In this task, we focus on improving site-specific beamforming. The objective is to evaluate the average SNR of synthesized beams using different dataset augmentation methods. Our aim is to maximize the SNR with minimal training data. We utilize a deep learning-based beam alignment engine (BAE) [3] as the primary method for this purpose, with detailed descriptions omitted for brevity.
Result of Downstream task 2
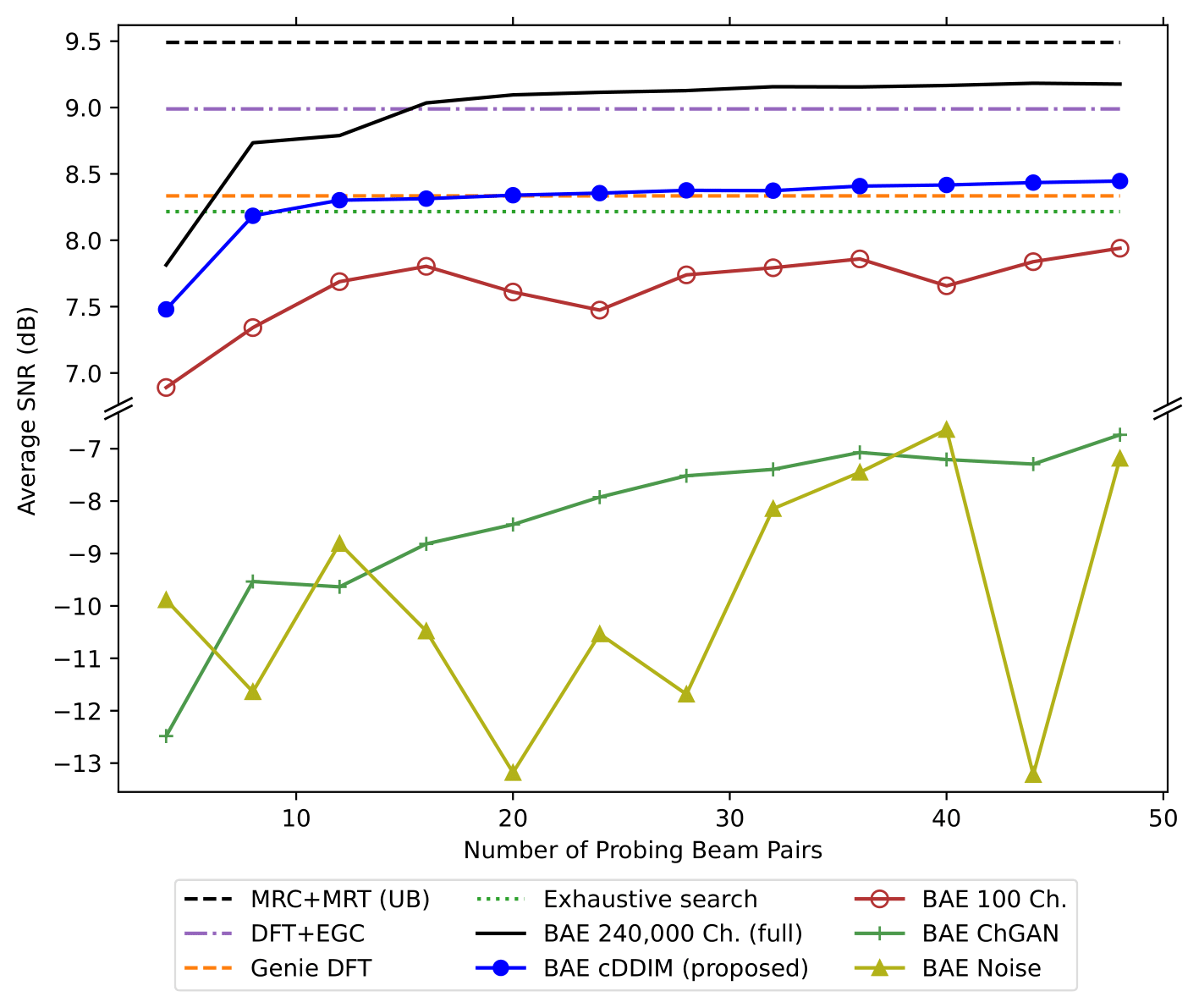
The BAE trained with the dataset augmented by cDDIM (blue line with circle markers) shows significantly higher average SNR compared to datasets augmented by ChannelGAN (green solid line with plus markers) or Gaussian noise (yellow solid line with triangle markers). Using more than 16 beams in cDDIM-based augmentation consistently outperforms exhaustive search and the Genie DFT case, demonstrating that deep learning-based methods trained to optimize beam selection with grid-free beams provide improved average SNR.
Other methods, such as ChannelGAN and adding noise, exhibit significantly worse SNR, indicating that these augmentation methods do not produce datasets conducive to good beamforming results.
For a detailed explanation, please refer to our upcoming paper.
References
[1] Generating High Dimensional User-Specific Wireless Channels using Diffusion Models, Taekyun Lee, Juseong Park, Hyeji Kim, and Jeffrey G. Andrews. To be submitted.
[2] Multi-resolution CSI feedback with deep learning in massive MIMO system, Zhilin Lu, Jintao Wang, Jian Song. International Conference on Communications (ICC), 2020.
[3] Grid-free MIMO beam alignment through site-specific deep learning, Yuqiang Heng, Jeffrey G. Andrews, IEEE Trans. Wireless Commun., 2023.