Interference Channels
A two-user interference channel is a canonical model for multiple one-to-one communications, where two transmitters wish to communicate with their receivers via a shared medium, examples of which include pairs of base stations and handsets near the cell boundary that suffer from interference. Practical codes and the fundamental limit of communications are unknown for interference channels as mathematical analysis becomes intractable. Hence, simple heuristic coding schemes are used in practice to mitigate interference, e.g., time division, treating interference as noise, and successive interference cancellation. These schemes are nearly optimal for extreme cases: when interference is strong or weak. However, there is no optimality guarantee for channels with moderate interference. Here we combine deep learning and network information theory to overcome the limitation on the tractability of analysis and construct finite-blocklength coding schemes for channels with various interference levels. We show that carefully designed and trained neural codes using network information theoretic insight can achieve several orders of reliability improvement for channels with moderate interference.
Problem Setup
The problem setup is illustrated below. We focus on the symmetric two-user real Additive White Gaussian Noise (AWGN) interference channel, i.e. \(\textbf{Y}_1 = \textbf{C}_1 + h \textbf{C}_2 + \textbf{Z}_1, \textbf{Y}_2 = \textbf{C}_2 + h \textbf{C}_1 + \textbf{Z}_2\), where \(\textbf{Z}_1, \textbf{Z}_2 \sim \mathcal{N}(0,\sigma^2I)\), \(\mathbf{C}_i\) denotes the \(i\)-th encoder’s transmitted signal, and \(h\) is the interference coefficient. We assume that each encoder has a length \(K\) random binary sequence to communicate, i.e., \(\mathbf{b}_i \in [0,1]^K\) and generates a codeword of length \(n\), \(\mathbf{C}_i \in \mathbb{R}^n\). The \(i\)-th decoder estimates the desired message \(\mathbf{\hat{b_i}} \in [0,1]^K\) based on \(\mathbf{Y}_i \in \mathbb{R}^n\).

The encoders and decoders are replaced by TurboAE encoders and decoders respectively, described below.
Background on Turbo Autoencoder (TurboAE)
In this section, we review Turbo Autoencoder (TurboAE) [2], one of the state-of-the-art neural network-based channel codes for point-to-point AWGN channels.
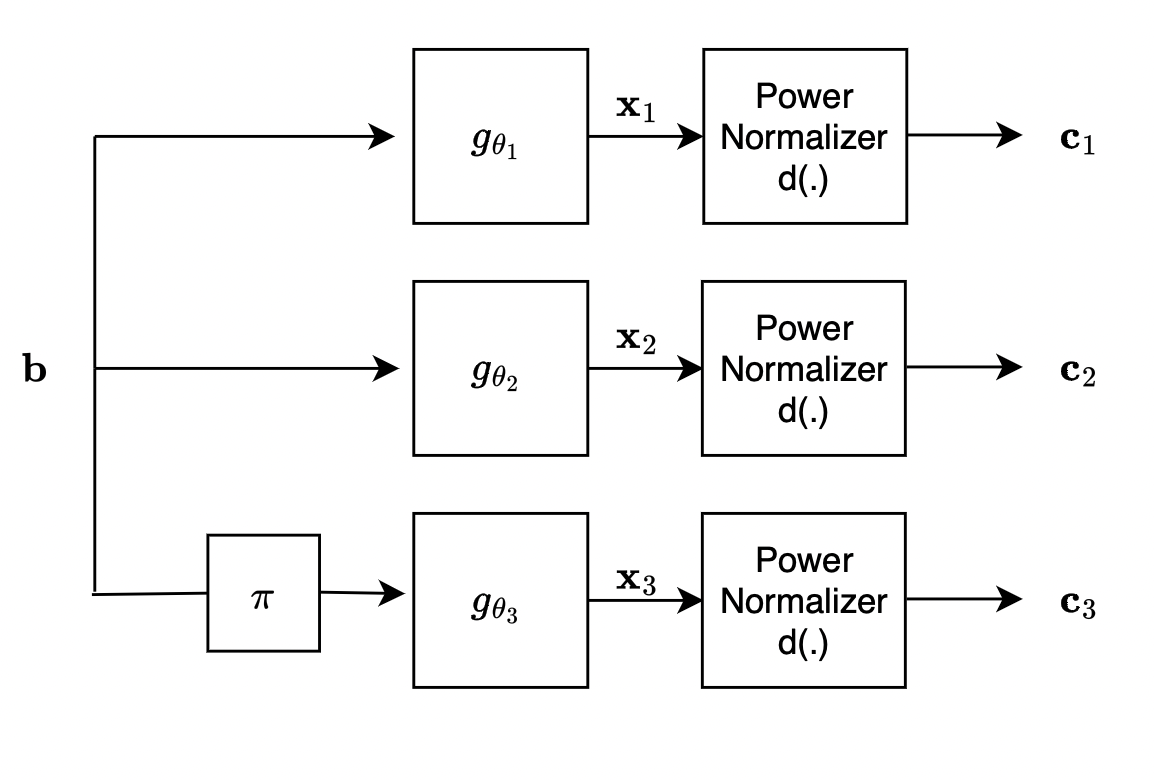
The encoder consists of three learnable blocks \(g_{\theta_1}\), \(g_{\theta_2}\) and \(g_{\theta_3}\) placed in parallel, followed by a power normalizing layer \(d(.)\). Each learnable block consists of a 1-D CNN followed by a linear layer. For the upper two branches, each message sequence \(\textbf{b}\) is encoded into 2 sequences \(\textbf{c}_1\) and \(\textbf{c}_2\). For the third branch, the message sequence \(\textbf{b}\) first goes through an interleaver \(\pi\) before being encoded into \(\textbf{c}_3\).
Inspired by the dynamic programming decoder, we let the decoder update the belief iteratively. Let \(\textbf{y}_1\), \(\textbf{y}_2\) and \(\textbf{y}_3\) be the noisy versions of \(\textbf{c}_1\), \(\textbf{c}_2\) and \(\textbf{c}_3\) respectively. The decoder goes through multiple iterations. Each iteration makes use of two sequential blocks of a 1-D CNN followed by a linear layer. At the last iteration, the message bits are estimated. The encoder and decoder architectures are shown below.
Encoder:
Decoder:

Training and Results
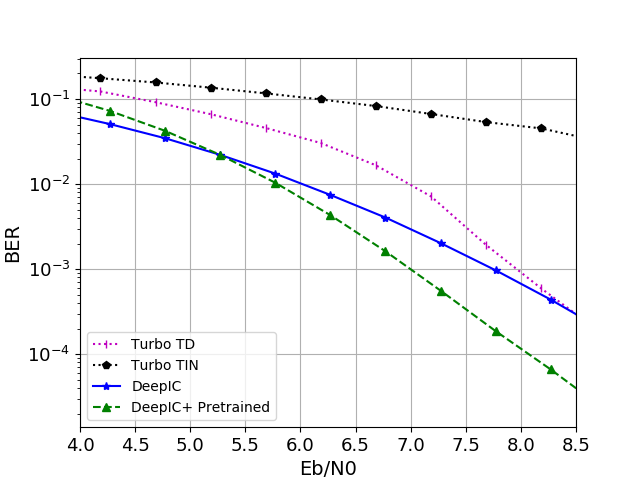
The training process consists of two phases. Initially, we pretrain a TurboAE encoder-decoder pair on a point-to-point AWGN channel. In the second phase, we transfer the pretrained models into the encoder-decoder pairs for the interference channel setup and fine-tune them under interference conditions. The results, presented in the figure below, plot the Bit Error Rate (BER) against Eb/N0. We compare the performance of several schemes: Time Division (Turbo TD), treating interference as noise (Turbo TIN), our proposed scheme with pretrained models (DeepIC+ Pretrained), and a previous version of our scheme without pretraining (DeepIC). The results indicate that our proposed scheme (DeepIC+ Pretrained) achieves the best performance among the evaluated methods.
Partial Time Division
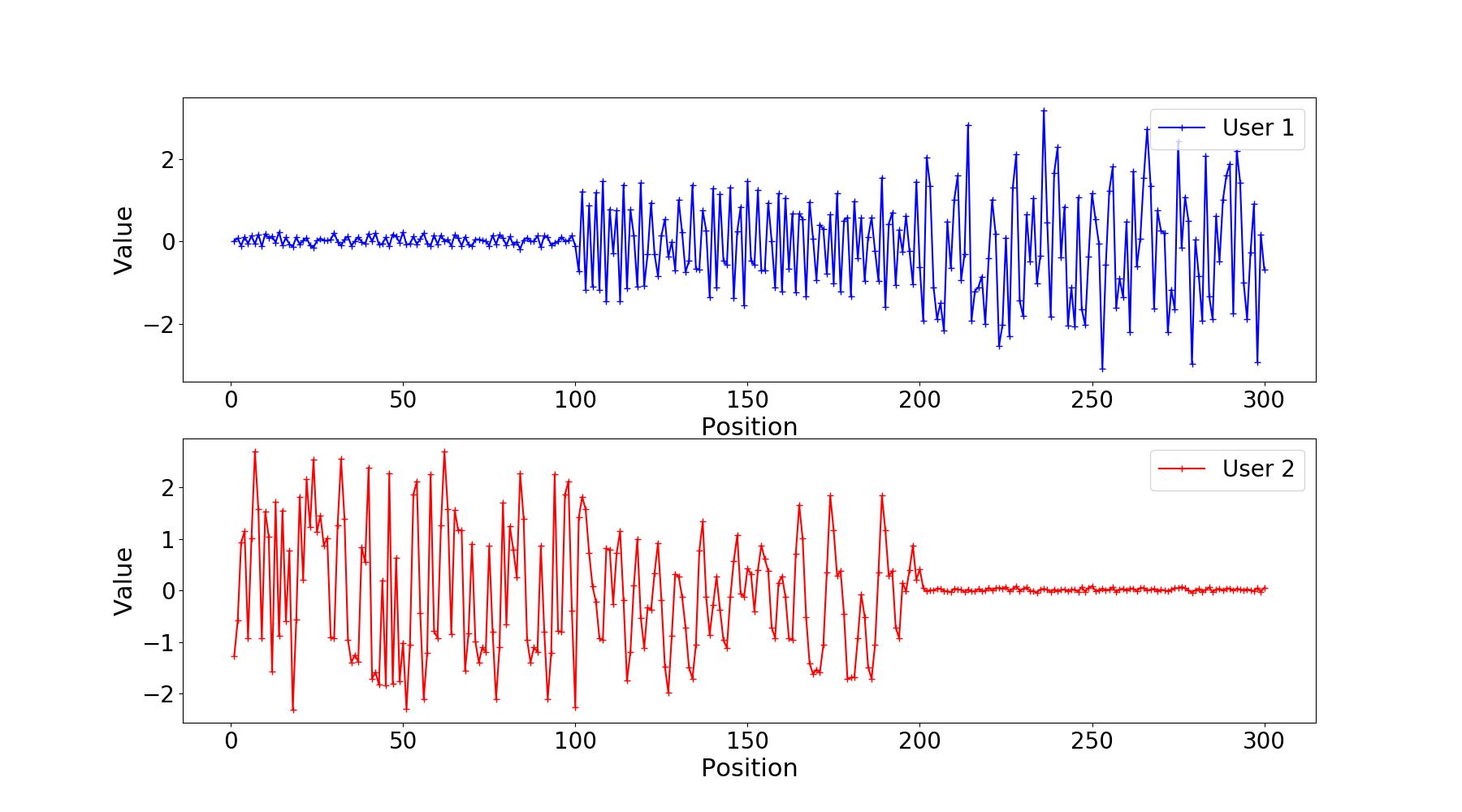
In the figure below, we plot the codewords \(\textbf{C}_1\) and \(\textbf{C}_2\) for randomly generated bit sequences \(\textbf{b}_1\) and \(\textbf{b}_2\) for \(K=100\) information bits and level of interference \(h=0.8\). We notice that DeepIC+ learned partial time division (TD). (Full TD happens in the first 100 and last 100 positions, while some joint coding happens in the middle 100 positions). We conjecture that the joint coding is the reason DEEPIC+ outperforms classical TD for h=0.8.
Finetuning Analysis
An important aspect of our model is the two-phase training. We investigate how the layers of the TurboAE encoders and decoders pre-trained on AWGN change after finetuning on the interference channel. This study will help us figure out which layers are being affected by the finetuning, alleviating us from training all the parameters of the model and only focusing on those specific layers. To measure the similarity between two networks, we use the Central Kernel Alignment (CKA) [3]. CKA measures the similarity between two sets of data representations by computing the alignment of their centered kernel matrices, providing a robust metric for comparing the learned features of different neural network layers or models. It effectively quantifies the degree to which two representations capture similar patterns in the data.
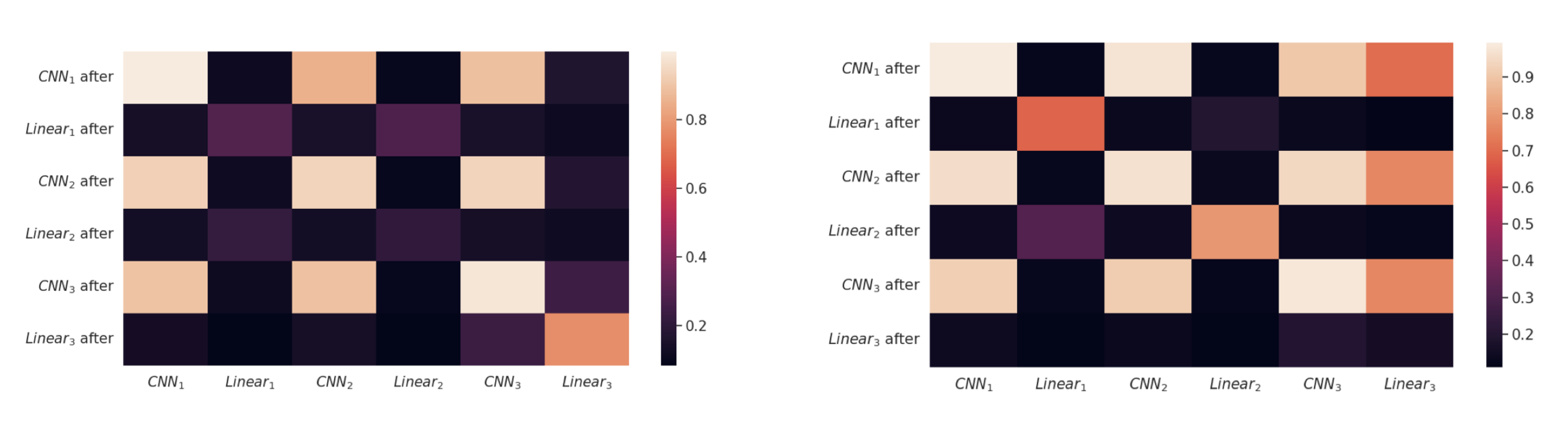
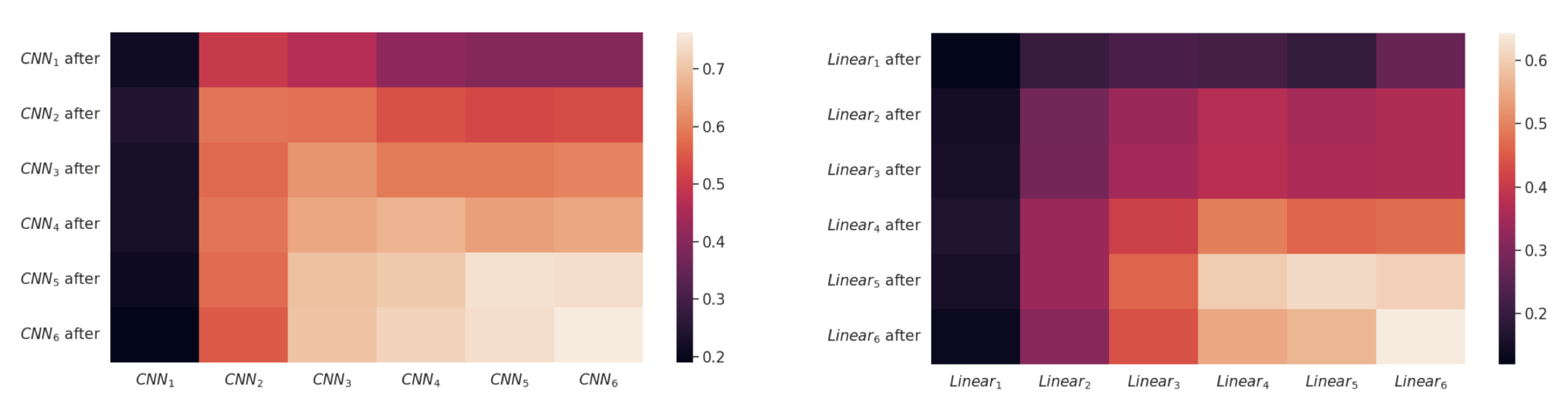
Encoders: as a reminder, the encoder consists of three learnable blocks, each consisting of a CNN followed by a linear layer, adding up to 6 neural layers to be analyzed. In the figures below, we plot the CKA similarity between each of the six neural layers before and after training on the interference channels for encoder 1 (left) and encoder 2 (right). Looking at the diagonal entries, we notice that for \(i \in \{1,2,3\}\) \(\text{CKA}(\text{CNN}_i,\text{CNN}_i \text{ after})\) has a value close to 1, while \(\text{CKA}(\text{Linear}_i,\text{Linear}_i \text{ after})\) has a lower score. We conjecture that finetuning on the interference channels affects the outermost linear layers only, keeping the CNNs unaltered.
Decoders: As previously mentioned, the decoder goes through multiple iterations. For each iteration, the decoder has two sequential blocks. Each block consists of a CNN followed by a linear layer. In our experiments, we use 6 iterations. We notice that the two sequential blocks show similar CKA performance and therefore show the results of the first block. In the figure below, we plot the CKA similarity score between the CNN layers (left) and linear layers (right) for each iteration before and after training on the interference channels. We notice similar CKA performances for the decoders of the two users and therefore show the results for one of the two. Based on the plot, we notice that the first few layers of the decoder change the most after finetuning, while the deeper layers gradually remain unchanged.
For a deeper understanding and further details, we encourage you to review our research paper.
References
[1] DeepIC+: Learning Codes for Interference Channels, Karl Chahine, Yihan Jiang, Joonyoung Cho, Hyeji Kim. IEEE Transactions on Wireless Communications, 2023.
[2] Turbo Autoencoder: Deep learning based channel codes for point-to-point communication channels, Yihan Jiang, Hyeji Kim, Himanshu Asnani, Sreeram Kannan, Sewoong Oh, Pramod Viswanath. NeurIPS, 2019.
[3] Similarity of neural network representations revisited, Simon Kornblith, Mohammad Norouzi, Honglak Lee, Geoffrey Hinton. ICML, 2019.