The unparalleled success of deep learning in various domains has revolutionized the way we approach problem-solving in areas such as computer vision and natural language processing. More recently, there has been significant progress in adapting these techniques to perform channel decoding, achieving impressive gains in performance and robustness. However, these gains come at a price. Deep learning models often demand significant computational resources and vast amounts of training data, making them challenging to deploy on resource-limited devices like mobile phones and IoT systems. That’s where hybrid techniques come into play, combining the benefits of both classical model-based methods and deep learning algorithms.
Model-based Machine Learning
Model-based machine learning is a scalable paradigm that leverages domain knowledge to achieve gains over traditional methods without significantly increasing complexity. The key idea is to augment model-based algorithms with learnable parameters, rather than replacing them by a black-box neural network. This blog post illustrates an application of model-based ML for improving the performance of Turbo decoding. But first, let’s briefly discuss channel coding and Turbo codes.
Setup : Channel coding
Consider communicating a message over a noisy channel. This communication system has an encoder that maps messages (e.g., bit sequences) to codewords, typically of longer lengths, and a decoder that maps noisy codewords to the estimate of messages. This is illustrated below.

Turbo codes
Turbo codes are a notable class of channel codes, developed in 1991 by Claude Berrou. The belief-propagation-based Turbo decoder achieves performance close to the theoretical (Shannon) limit, leading to the adoption of these codes in various communication standards, including cellular systems.
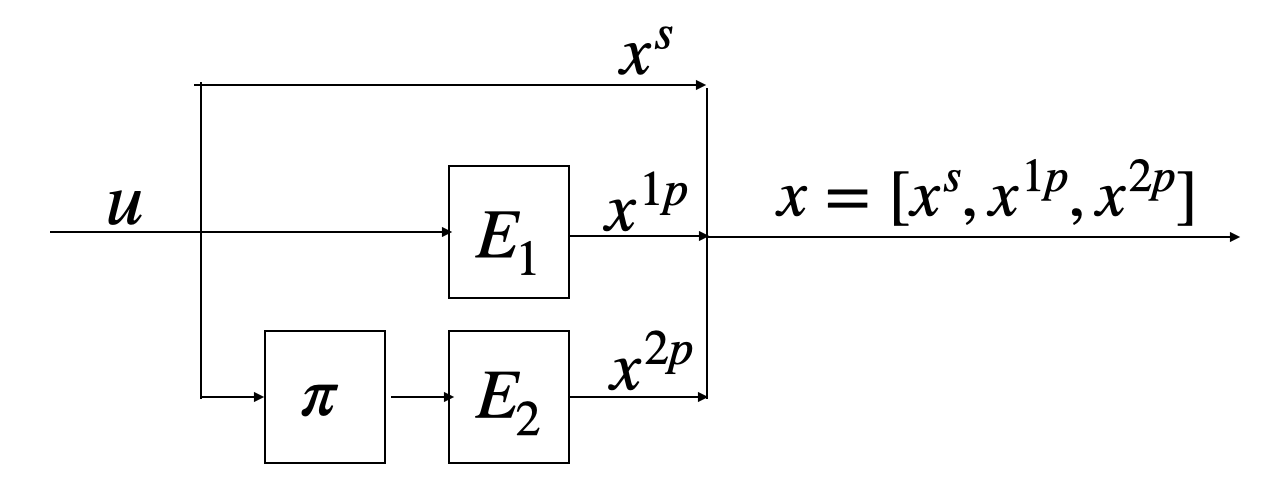
Turbo codes are sequential codes comprising of Recursive Systematic Convolutional (RSC) encoders, and an interleaver \(\pi\) as shown below. This code maps input u to \((x^s, x^{1p}, x^{2p})\). The systematic bit sequence \(x^s\) is equal to the input \(u\), while the parity bit sequences \(x^{1p}\) and \(x^{2p}\) are generated by the convolutional encoders \(E_1\) and \(E_2\) from \(u\) and the interleaved bit inputs \(\tilde{u} = \pi(u)\), respectively.
Turbo decoding
Convolutional codes can be optimally decoded using a Soft-in-Soft-out (SISO) decoding algorithm, such as the renowned BCJR algorithm. In the case of Turbo codes, the decoding process involves an iterative procedure that leverages the SISO decoders of the constituent convolutional codes, as depicted in the figure below. If you’re interested in an in-depth explanation of the BCJR algorithm, this resource provides an excellent description.
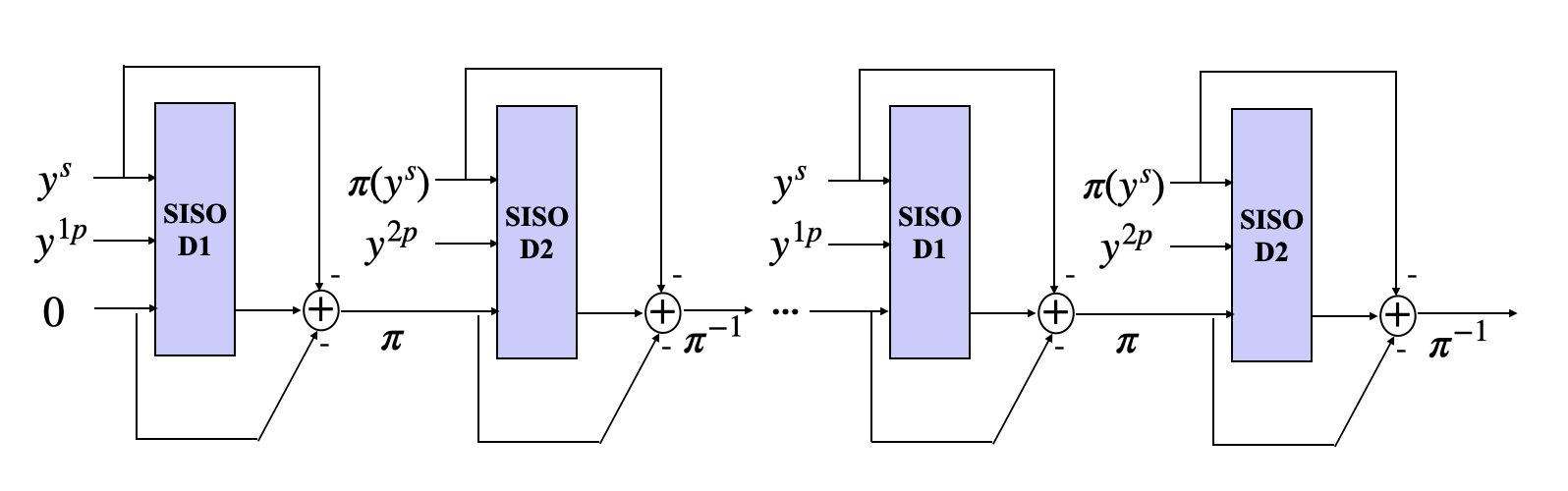
During Turbo decoding, two such SISO decoders \(D_1\) and \(D_2\) work together by exchanging extrinsic information, i.e., additional knowledge extracted by a SISO block in the current iteration of decoding. Notably, decoder \(D_1\) processes the systematic bits and parity bit 1, while Decoder \(D_2\) processes the interleaved systematic bits and parity bit 2, with each decoder extracting information from distinct parity bit streams to iteratively refine the posterior probability estimations \(L(u_k \vert y)\).
The extrinsic LLR \(L_e(u_k)\) is obtained as : \(L_e(u_k) = L(u_k \vert y) - L(y_k^s) - L(u_k) \quad k \in [K]\)
Here, \(L(u_k \vert y)\) is the posterior log-likelihood-ratio (LLR) estimate of the SISO decoding block, \(L(y_k^s)\) is the LLR of the received systematic symbols, while \(L(u_k)\) is the intrinsic LLR.
This extrinsic LLR is interleaved and passed to the next block as prior intrinsic information.
The BCJR algorithm involves computing the log-sum-exponential (LSE) function, which is computationally intensive. In practice, the max-log-MAP algorithm, an approximation of the MAP algorithm is employed as the SISO decoder. The main idea is to approximate the computationally intensive LSE function by the maximum:
\(\text{LSE}(z_1,\ldots, z_n) \triangleq \log (\exp(z_1)+\ldots+\exp(z_n))\) \(\text{LSE}(z_1,\ldots, z_n) \approx \max(z_1,\ldots, z_n), \quad z_1,\ldots,z_n \in \mathbb{R}.\)
While the max-log-MAP algorithm is more efficient than the MAP, it is less reliable.
TinyTurbo
In our pursuit to develop a decoder that is both efficient and reliable, we pose two crucial questions:
1) Is it feasible to design a decoder with complexity similar to max-log-MAP while maintaining the reliability of the MAP algorithm?
2) Can such a decoder generalize to non-AWGN noise and perform consistently across various blocklengths and encoding structures?
We answer these questions in the affirmative with the introduction of TinyTurbo, a model-based machine learning algorithm developed using a purely data-driven approach.
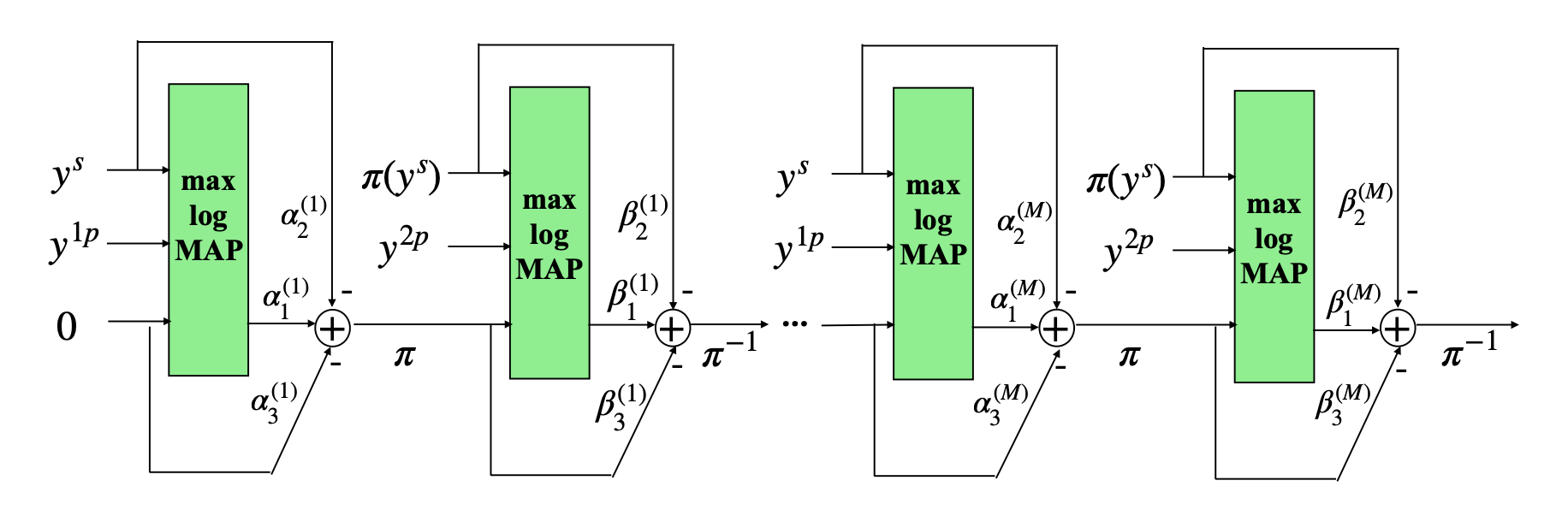
TinyTurbo is an adaptation of the max-log-MAP algorithm, incorporating three learnable weights within the extrinsic information equation of each SISO block. For instance, the extrinsic information of decoder \(D_1\) is obtained as \(L_e(u) = \alpha_1 L(u \vert y) - \alpha_2 y^s - \alpha_3 L(u)\). Similarly, decoder \(D_2\) is augmented by three weights \((\beta_1, \beta_2, \beta_3)\). As a result, TinyTurbo decoding with \(M\) iterations requires only \(6M\) parameters, maintaining comparable complexity as max-log-MAP.
We train these parameters to minimize the binary cross-entropy loss between message bits and their decoded estimates (a surrogate for the BER) using variants of stochastic gradient descent (SGD). This data-driven approach enables TinyTurbo to generalize across different channels, block lengths, and trellises.
TinyTurbo codebase
We provide a framework in Python to implement and evaluate different Turbo decoders, and implement model-based ML methods like TinyTurbo. The project repository and running instructions can be found here. Further, we provide an intuitive interface for inference and training of TinyTurbo in the deepcommpy package.
The code snippet below demonstrates how to use this package for Turbo code decoding inference for Turbo-LTE, block length 40:
import torch
import deepcommpy
from deepcommpy.utils import snr_db2sigma
from deepcommpy.channels import Channel
# Create a Turbo code object : Turbo-LTE, Block_length = 40
block_len = 40
turbocode = deepcommpy.tinyturbo.TurboCode(code='lte', block_len = block_len)
# Create an AWGN channel object.
# Channel supports the following channels: 'awgn', 'fading', 't-dist', 'radar'
# It also supports 'EPA', 'EVA', 'ETU' with matlab dependency.
channel = Channel('awgn')
# Generate random message bits for testing
message_bits = torch.randint(0, 2, (10000, block_len), dtype=torch.float)
# Turbo encoding and BPSK modulation
coded = 2 * turbocode.encode(message_bits) - 1
# Simulate over range of SNRs
snr_range = [-1.5, -1, -0.5, 0, 0.5, 1, 1.5, 2]
for snr in snr_range:
sigma = snr_db2sigma(snr)
# add noise
noisy_coded = channel.corrupt_signal(coded, sigma)
received_llrs = 2*noisy_coded/sigma**2
# Max-Log-MAP Turbo decoding with 3 iterations
_ , decoded_max = turbocode.turbo_decode(received_llrs, number_iterations = 3, method='max_log_MAP')
# MAP Turbo decoding with 6 iterations
_ , decoded_map = turbocode.turbo_decode(received_llrs, number_iterations = 6, method='MAP')
# TinyTurbo decoding with 3 iterations
_, decoded_tt = turbocode.tinyturbo_decode(received_llrs, number_iterations = 3)
# Compute the bit error rates
ber_max = torch.ne(message_bits, decoded_max).float().mean().item()
ber_map = torch.ne(message_bits, decoded_map).float().mean().item()
ber_tt = torch.ne(message_bits, decoded_tt).float().mean().item()
Results
We evaluate the performance of TinyTurbo, running for three decoding iterations, by comparing it against two baselines: the efficient max-log-MAP decoder with three decoding iterations, and the MAP decoder with six iterations, which is near-optimal for the codes considered.
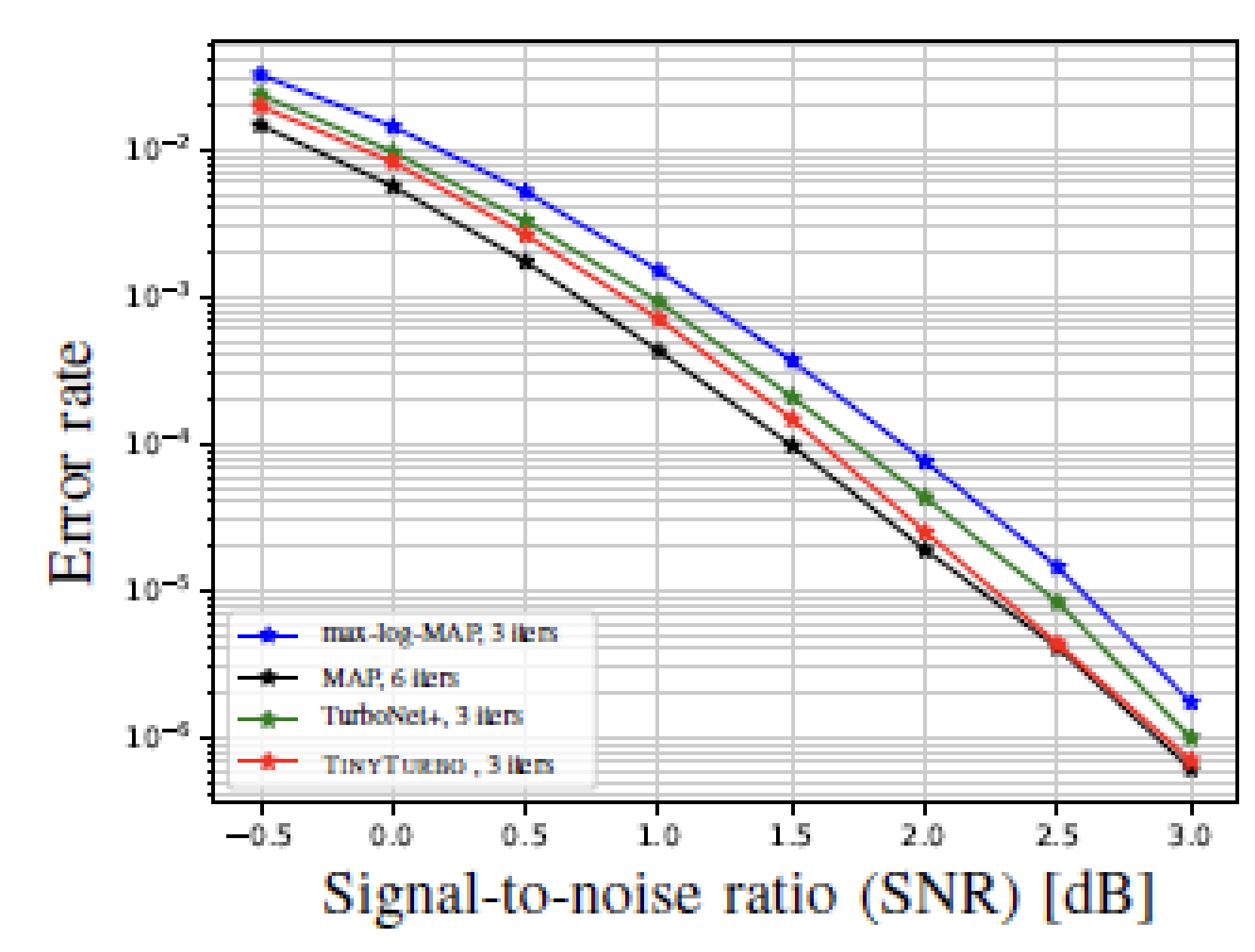
We observe that TinyTurbo achieves a performance close to that of the MAP decoder while maintaining a decoding complexity comparable to the suboptimal max-log-MAP decoder. This highlights the effectiveness of our proposed algorithm.
Moreover, TinyTurbo demonstrates remarkable generalization capabilities. For example, as demonstrated below, when trained on Turbo-LTE of block length 40, it successfully generalizes to a block length of 200, as well as to the Turbo-757 code. This showcases the flexibility of the TinyTurbo approach across different code structures and lengths.
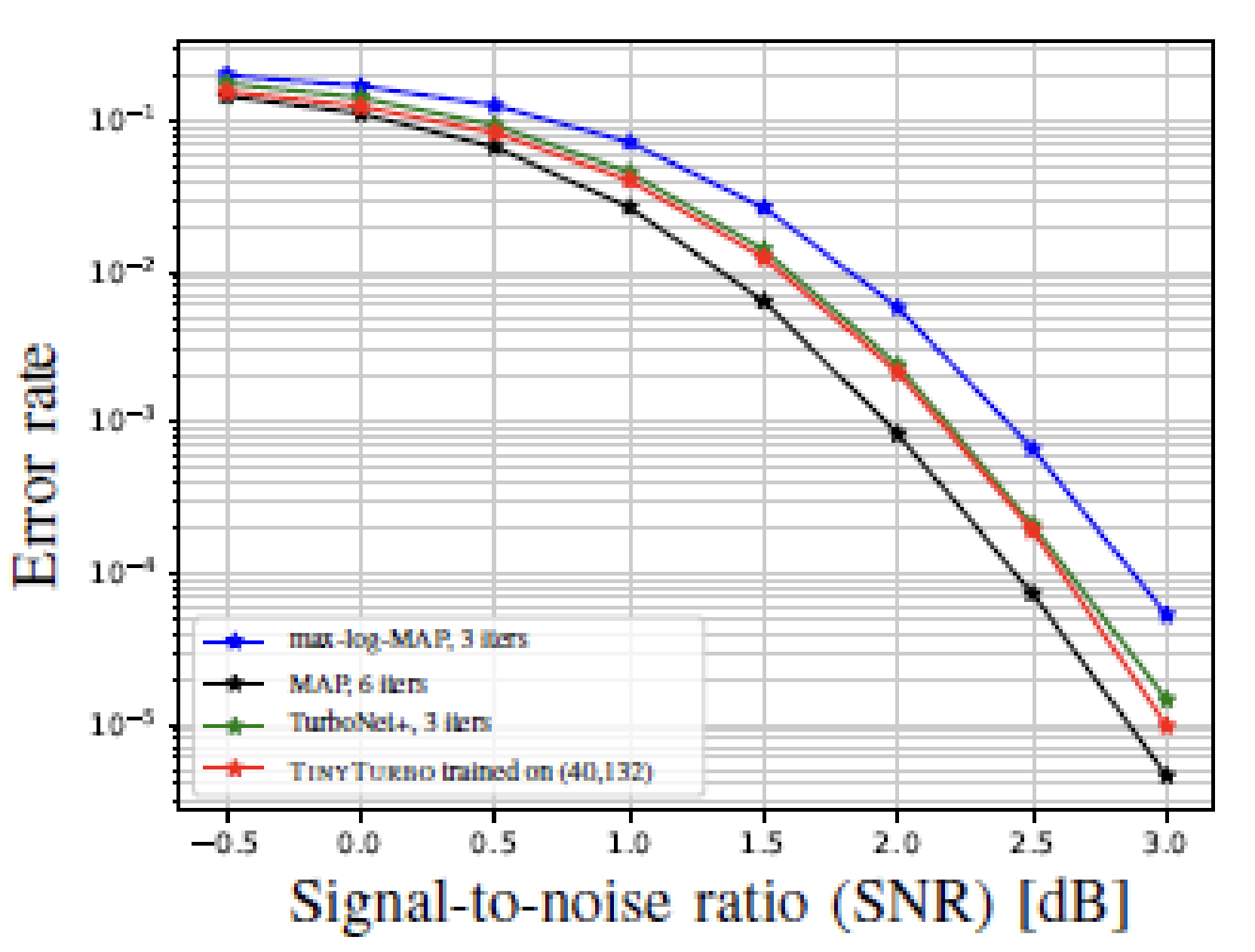 |
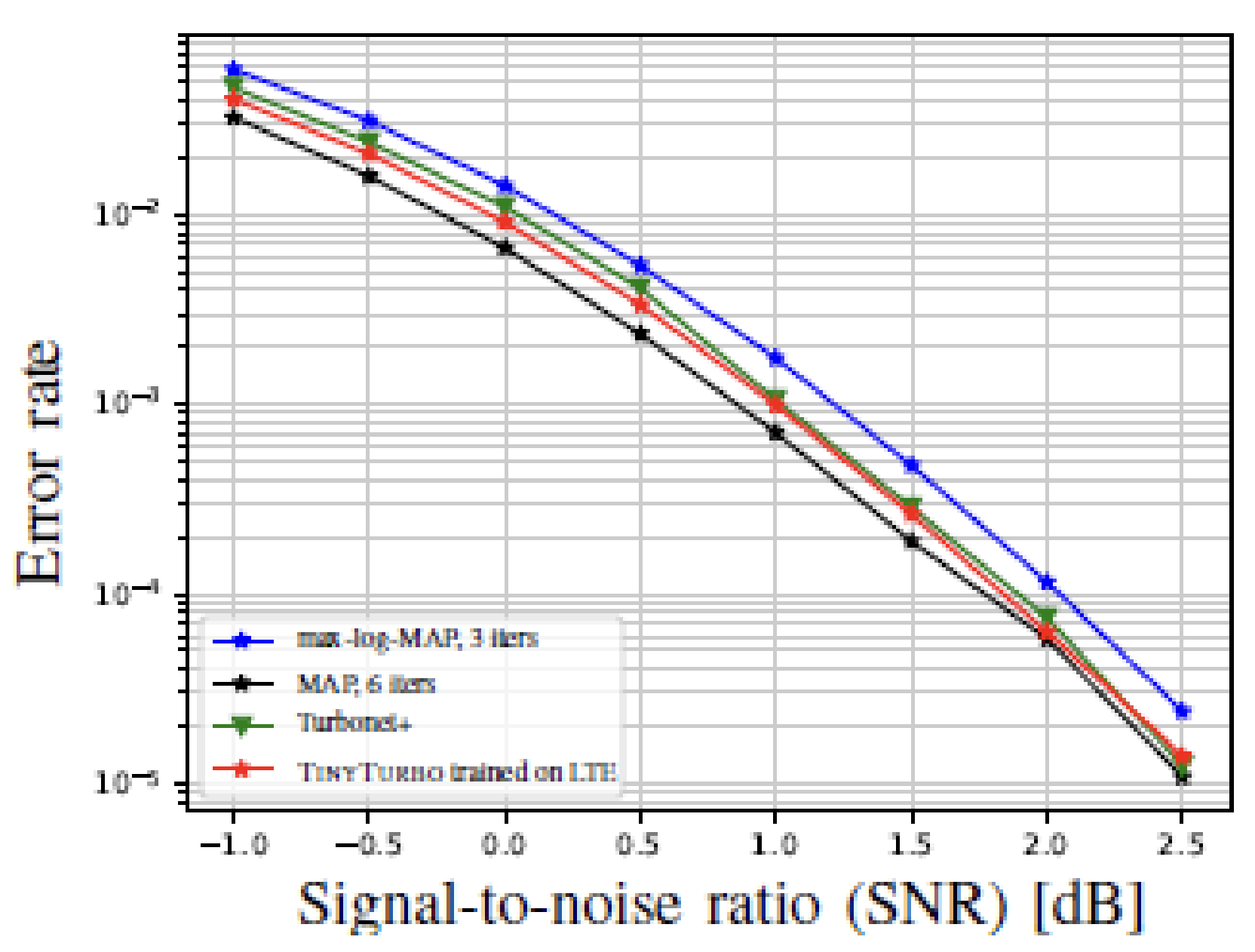 |
Notably, like other data-driven decoders, TinyTurbo exhibits robustness against deviations from AWGN noise. In tests on a channel with bursty noise, TinyTurbo outperforms both of the baselines considered, emphasizing its ability to handle varying noise conditions. Additionally, TinyTurbo also exhibits substantial gains when tested on the multi-path fading EPA (Extended Pedestrian A) channel, further emphasizing its adaptability and effectiveness in various scenarios.
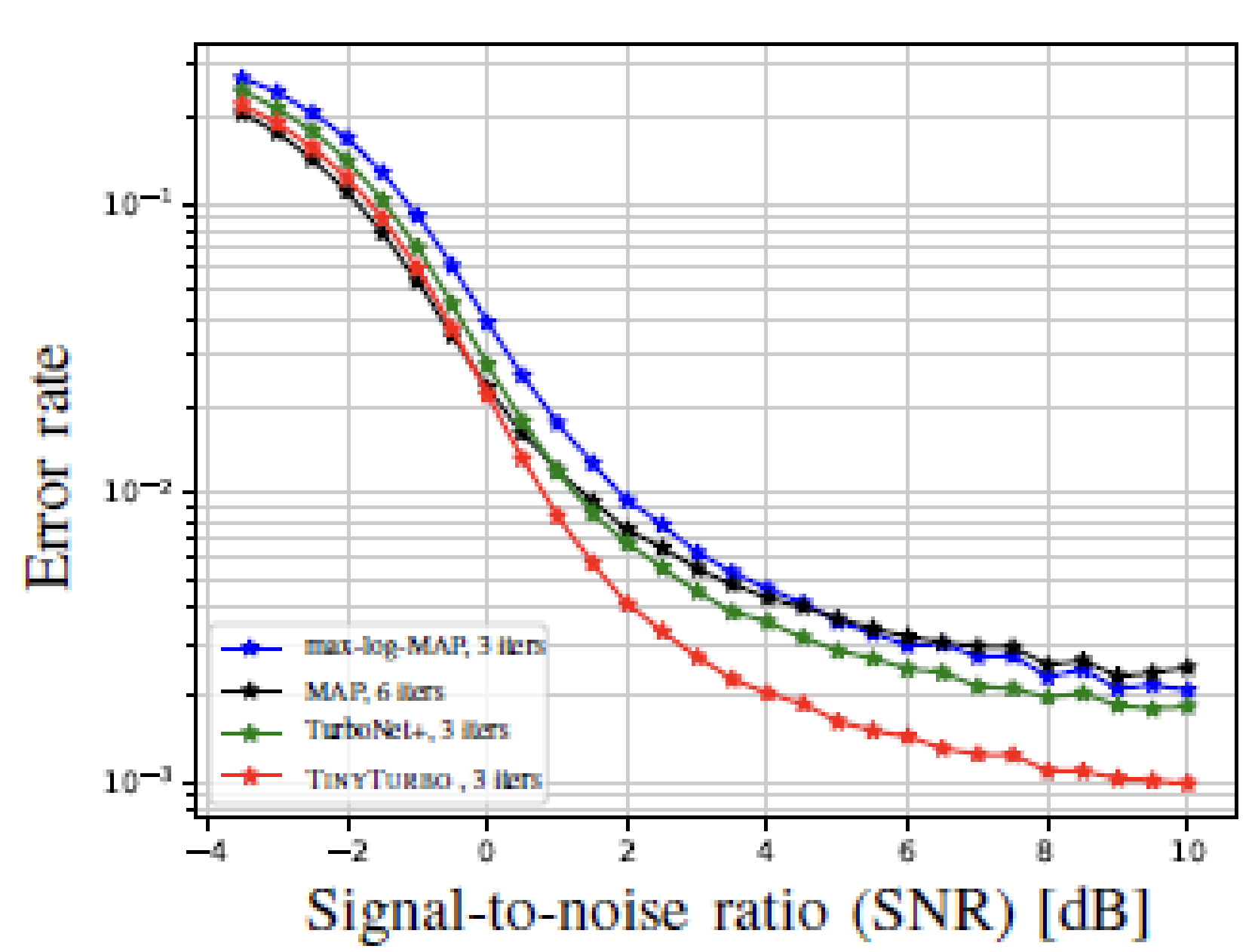 |
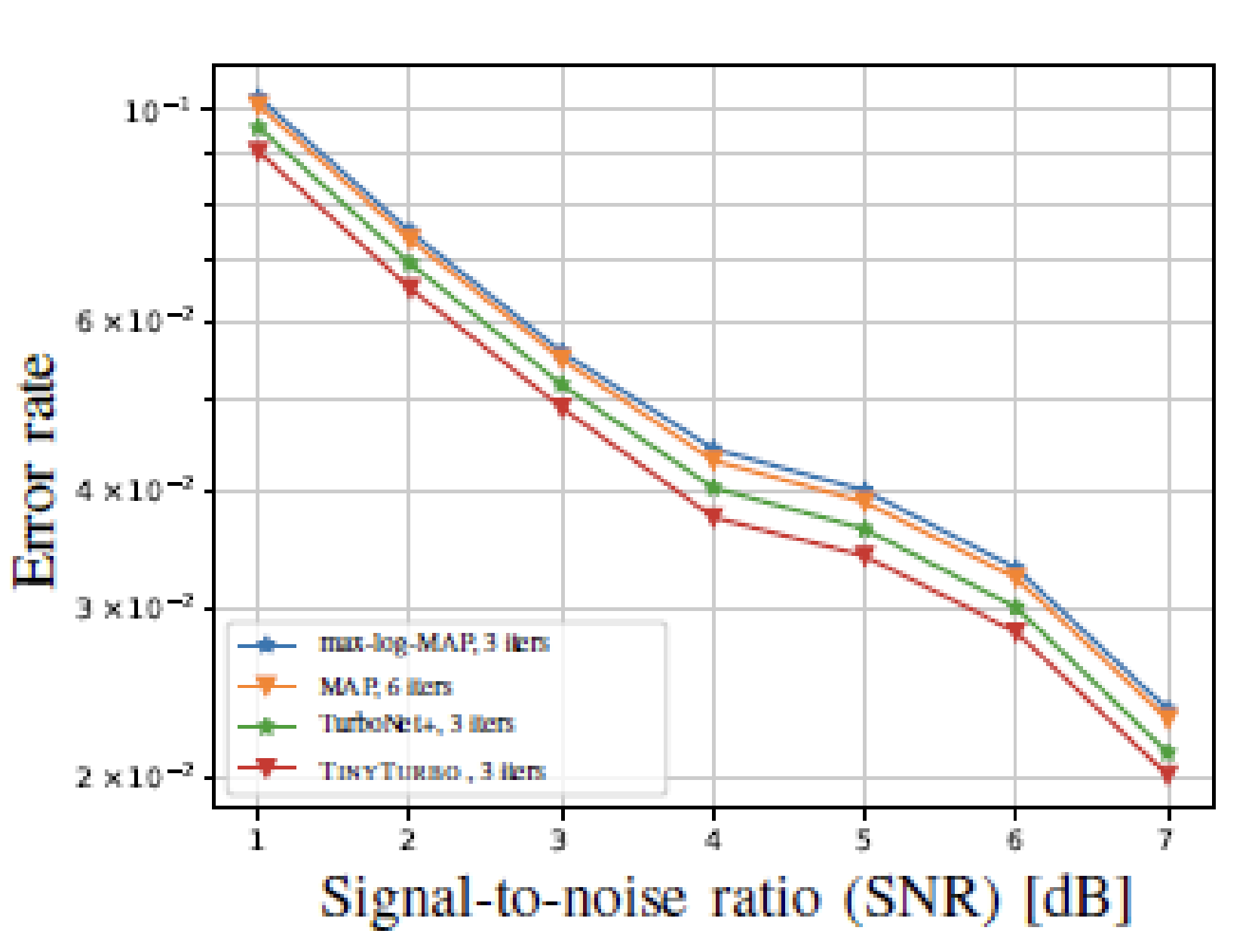 |
For a more comprehensive analysis and additional details, we invite you to read our research paper.
References
TinyTurbo: Efficient Turbo Decoders on Edge, Ashwin Hebbar, Rajesh Mishra, Sravan Kumar Ankireddy, Ashok Makkuva, Hyeji Kim, Pramod Viswanath. ISIT 2022