This two-part blog post aims to provide a gentle introduction to recent work showing the efficacy of using machine learning to design coded computation schemes. We start with a background on coded computation and its challenges, and discuss the possibility of using machine learning to overcome these challenges. We then describe our recent work toward leveraging machine learning to extend the reach of coded computation. We conclude by sharing our views on future directions for learning-based coded computation.
Along the way, we showcase how one can easily explore learning-based coded computation using the framework that we have made available on Github. If you’re interested in using this code, we encourage you to visit our Github repository, and to raise an issue to ask questions, ask for help, or provide suggestions – we are looking forward to actively interacting with the community in this space!
Distributed computing and coded computation
Distributed computing has become pervasive in increasing the scale of common applications, such as machine learning training and inference, data analytics, and scientific simulations. However, many distributed computing environments are prone to unpredictable slowdowns and failures that can jeopardize application-level performance. There are many causes of such slowdowns and failures, such as contention for compute and network resources, or hardware wearout and failure. Left unmitigated, these unpredictable slowdowns and failures can inflate job completion times or cause online services to violate strict latency agreements.
Provisioning extra resources to perform redundant computations is a common strategy for alleviating the effects of unpredictable slowdowns and failures, but often comes with high resource overhead. The de-facto approach to redundancy in distributed computing systems is replication, wherein multiple copies of the same computation are performed on different servers, and the result of computation is taken from the fastest of the replicas. However, a system that provisions R additional replicas has R-times resource overhead; even with small values of R, this can be more redundancy than operators are willing to pay.
Coded computation: low-overhead tolerance of slowdowns and failures
Coded computation is an emerging solution class that applies techniques from the domain of coding theory to alleviate the effects of slowdowns and failures in distributed computing systems in a resource-efficient manner. While the idea of using coding-theoretic tools to perform computation on unreliable hardware has been studied for decades, the use of such tools in large-scale distributed systems has only more recently been studied, initiated by Lee et al. We will now describe the general coded computation setup, which is illustrated in the figure below:
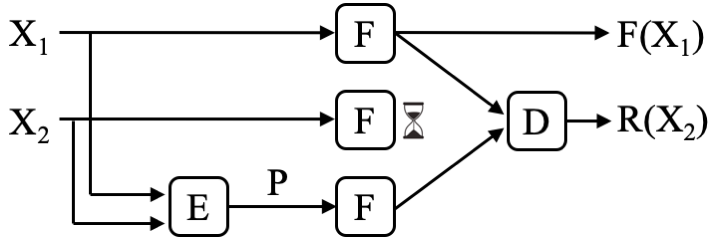
Suppose that k instances of a computation F are performed on separate servers (k = 2 in the figure). Each input Xi, is sent to one of the instances of F to compute and return F(Xi). Thus, given k inputs X1, X2, …, Xk, the goal is to compute F(X1), F(X2), …, F(Xk). As depicted in the above figure, coded computation introduces an encoder E, a decoder D, and r additional instances of F (in the figure, r = 1). The encoder E takes in k original inputs X1, X2, …, Xk and produces r parities P1, P2, …, Pr. All original and parity inputs are sent to distinct instances of F. Given any k out of the total (k+r) original and parity outputs from instances of F, the decoder D reconstructs the original k outputs F(X1), F(X2), …, F(Xk). We denote a reconstructed output for input Xi by R(Xi). This setup can recover from up to r slow or failed computations.
In the figure above with k = 2 and r = 1, coded computation could potentially reconstruct any one of the two function outputs while using only one redundant server. In contrast, a replication-based approach would require two redundant servers to tolerate the same number of slow or failed servers. Thus, coded computation can tolerate slowdowns and failures using significantly less resource overhead than replication-based approaches.
Key challenge in coded computation: handling general nonlinear functions
While coded computation offers the promise of low-overhead tolerance of slowdowns and failures, current approaches are applicable only for restricted classes of computations. A vast majority of existing coded-computation schemes are applicable only for linear (and in some cases multilinear) functions, for example, matrix-vector multiplication and matrix-matrix multiplication. Recent work by Yu et al. supports multivariate polynomials. Applying coded computation to general nonlinear functions beyond these classes of functions had remained open. This is, in fact, a key barrier to the wider adoption of coded computation since many functions of interest are nonlinear, such as neural networks in machine learning inference systems.
Extending the reach of coded computation via learning
Our goal is to enable coded computation for general nonlinear functions, such as neural networks in machine learning inference systems.
Machine learning has recently led to significant advances in complex tasks, such as image classification and natural language processing. This leads one to question: can machine learning similarly help overcome the challenges of performing coded computation for nonlinear functions?
We have taken the first steps toward answering this question in the affirmative by proposing and evaluating a learning-based coded computation framework. We have developed two distinct paradigms for leveraging machine learning for designing coded-computation schemes:
- Learning a code: using neural networks as encoders and decoders to learn a code that enables coded computation over nonlinear functions.
- Learning a parity computation: using simple encoders and decoders (e.g., addition/subtraction, concatenation), and instead learning a new computation over parities that enables reconstruction of unavailable outputs.
The techniques that we develop have the potential for applicability to a broad class of computations. For concreteness, we focus on imparting resilience to machine learning models during inference, specifically, neural networks. Inference is the process of using a trained machine learning model to produce predictions in response to input queries. Large-scale services typically perform inference in so-called “prediction-serving systems” in which multiple servers run a copy of the same machine learning model and queries are load-balanced across these servers. We focus on inference because it is commonly deployed in latency-sensitive services in which slowdowns and failures can jeopardize user experience. Neural network inference also represents a challenging nonlinear computation for which previous coded computation approaches are inapplicable. While neural networks do contain linear components (e.g., matrix multiplication), they also contain many nonlinear components (e.g., activation functions, max pooling), which make the overall function computed by the neural network nonlinear.
Using machine learning for coded computation leads to the reconstruction of approximations of unavailable results of computation. This is appropriate for imparting resilience to inference, as the results of inference are themselves approximate. Furthermore, any inaccuracy incurred due to employing learning only comes into play when a result from inference would otherwise be slow or failed. In this case, many services prefer a slightly less accurate result as compared to a late one.
In the remainder of this post and in the next post, we describe the two different paradigms we have developed for leveraging machine learning for designing coded-computation schemes. For a more detailed description comparing the two approaches, we direct the reader to our paper Learning-Based Coded Computation.
Paradigm 1: Learning a code
We now describe our first approach for learning-based coded computation: learning erasure codes. Recall that the coded-computation setup described above has three components: the given function F, the encoder E, and the decoder D. Under this paradigm, we learn an encoder E and a decoder D that accurately reconstruct unavailable outputs from the given function F. We use neural networks to learn the encoder and the decoder for a given function F due to their recent success in a number of learning tasks.
The goal of training is to learn a neural network encoder E and neural network decoder D that accurately reconstruct unavailable function outputs. The given function F is not modified during training.
When the given function F is a machine learning model, the encoder and the decoder are trained using the same training dataset that was used to train F. When such a dataset is not available, which will be the case for generic functions F outside the realm of machine learning, one can instead generate a training dataset comprising pairs (X, F(X)) for values of X in the domain of F. Each sample for training the encoder and decoder uses a set of k (randomly chosen) inputs from the training dataset. A forward and backward pass is performed for each of the [(k+r) choose r] possible unavailability scenarios, except for the case in which all unavailable outputs correspond to parity inputs. An iterative optimization algorithm, such as stochastic gradient descent, updates the encoder and decoder’s parameters during training.
A forward and a backward pass under this training setup is illustrated below (where k = 2 and r = 1).
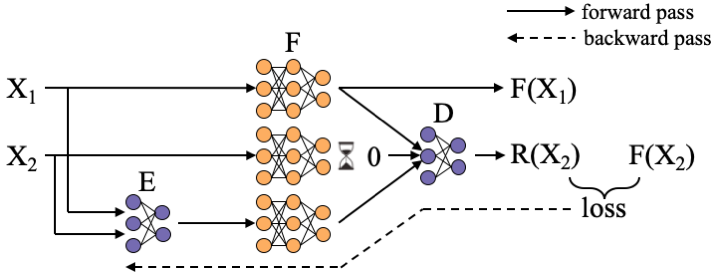
During a forward pass, the k data inputs X1, X2, …, Xk are fed through the encoder to generate r parity inputs P1, P2, …, Pr. Each of the (k+r) inputs (data and parity) are then fed through the given function F. The resulting (k+r) outputs F(X1), F(X2), …, F(Xk), F(P1), F(P2), …, F(Pr) are fed through the decoder D, and up to r of these outputs are simulated to be unavailable by replacing their values with a vector of all zeros. The decoder produces (approximate) reconstructions for the unavailable function outputs among F(X1), F(X2), …, F(Xk). A backward pass involves using any chosen loss function (e.g., mean squared error) and backpropagating through D, F, and E. We train the encoder and decoder in tandem by backpropagating through F, making this approach applicable to any numerical differentiable function F. We note, however, that F remains fixed throughput training; only the encoder E and D are learned.
Many loss functions can be used in training encoders and decoders. For simplicity, we use as a loss function the mean squared error between the reconstructed output R(X) and the output F(X) that would be returned if the original model were not slow or failed. This loss function is general enough to be applicable to many functions F. A loss function that is specific to F may also be used, such as cross-entropy loss for image classification tasks.
We have experimented with convolutional neural networks (CNNs) and multilayer perceptrons (MLPs) as neural network encoders and decoders. Our experiments show the greatest success when using a CNN encoder and a MLP decoder. Interestingly, as an aside, we found that a special form of convolution called “dilated convolution” is particularly well-suited for use in CNN encoders for image-related functions, such as image classification. This type of convolution allows one to encode pixels that are farther apart spatially while using fewer parameters than a traditional convolution.
We evaluate the proposed approach in reconstructing unavailable outputs resulting from a ResNet-18 neural network on several image classification tasks: CIFAR-10, Fashion-MNIST, and MNIST. With k = 2 and r = 1, that is, using half of the redundant resources as a replication-based approach, we find that the reconstructed predictions resulting from this approach have an accuracy of 0.7%, and 11.4% lower than if the original model’s predictions were always available on the Fashion-MNIST and CIFAR-10 datasets; the best encoder and decoder pair on the MNIST dataset experienced no loss in accuracy. These are promising results for learning-based coded computation, considering that prior coded-computation schemes are inapplicable to even simple neural networks.
There are many additional interesting things to share about learned encoders and decoders for coded computation that we simply don’t have the space to cover in this blog post. For more details, please see our full report on this work in our paper. We have also made the codebase used for evaluating learned encoders and decoders available on Github, including detailed comments and all hyperparameters used in the paper.
Codebase for experimenting with learned encoders and decoders
As described above, our framework for experimenting with learned encoders and decoders is available on Github, with detailed instructions. Experimenting using this framework is quite simple, as we will illustrate below.
You can run an example of training learned encoders and decoders on your laptop using these instructions, and using the mnist_learned.json configuration file. This requires only a few simple instructions, and should take only a few minutes to get running.
We have also made implementing and experimenting with different encoders and decoders using our framework simple. The code snippet below shows all that is needed to implement the MLP-based encoder that we explored in this work.
from torch import nn
from coders.coder import Encoder, Decoder
from util.util import get_flattened_dim
class MLPEncoder(Encoder):
def __init__(self, ec_k, ec_r, in_dim):
"""
Arguments
---------
ec_k: int
Parameter k to be used in coded computation
ec_r: int
Parameter r to be used in coded computation
in_dim: list
List of sizes of input as (batch, num_channels, height, width).
"""
super().__init__(ec_k, ec_r, in_dim)
# The MLP encoder flattens image inputs before encoding. This function
# gets the size of such flattened inputs.
self.inout_dim = get_flattened_dim(in_dim)
# Set up the feed-forward neural network consisting of two linear
# (fully-connected) layers and a ReLU activation function.
self.nn = nn.Sequential(
nn.Linear(in_features=ec_k * self.inout_dim,
out_features=ec_k * self.inout_dim),
nn.ReLU(),
nn.Linear(in_features=ec_k * self.inout_dim,
out_features=ec_r * self.inout_dim)
)
def forward(self, in_data):
# Flatten inputs
val = in_data.view(in_data.size(0), -1)
# Perform inference over encoder model
out = self.nn(val)
# The MLP encoder operates over different channels of input images
# independently. Reshape the output to to form `ec_r` output images.
return out.view(out.size(0), self.ec_r, self.inout_dim)
Encoders and decoders derive from Encoder and Decoder base classes, which themselves are
simply lightweight wrappers around PyTorch nn.Modules. As a result,
one needs only to construct their desired neural network structure and implement the forward
method – PyTorch will automatically perform the differentiation needed for training.
Trying out new encoders and decoders is also straightforward in our framework. Once you’ve
implemented your encoder or decoder, simply change the encoder/decoder type in the enc_dec_types
field of the configuration file you are using. For example, we can run the same MNIST training
example performed above, but with the ConvEncoder with the following change to the mnist_learned.json configuration file:
{
"num_epoch": 500,
"k_vals": [2, 3, 4],
# Change the following line to: "enc_dec_types": [["coders.conv.ConvEncoder", "coders.mlp.MLPDecoder"]],
"enc_dec_types": [["coders.mlp.MLPEncoder", "coders.mlp.MLPDecoder"]],
"datasets": ["mnist"],
"models": ["base-mlp"],
"losses": ["torch.nn.MSELoss"],
"train_encoder": true,
"train_parity_model": false,
"train_decoder": true
}
Conclusion of Part 1
This concludes the first part of this blog post on learning-based coded computation. We have introduced coded computation and its potential benefits, the challenges that limit prior state-of-the-art, and the potential for learning-based approaches to overcome these challenges. We then described the first of the two paradigms that we propose toward leveraging machine learning for designing coded computation schemes: learning encoders and decoders. Along the way, we’ve illustrated how you can experiment with learned encoders and decoders using our framework made available on Github.
In Part 2 of this blog post, we will explore the second approach to learning-based coded computation: employing simple encoders and decoders, and instead learning a new computation over parities. We will also describe potential avenues for future exploration in learning-based coded computation, and how one can immediately begin experimenting with them in our framework.
References to papers described in Part 1
Learning-Based Coded Computation. Jack Kosaian, K. V. Rashmi, and Shivaram Venkataraman. In IEEE Journal on Selected Areas in Information Theory, 2020.
Learning a Code: Machine Learning for Approximate Non-Linear Coded Computation. Jack Kosaian, K. V. Rashmi, and Shivaram Venkataraman. arXiv preprint arXiv:1806.01259, 2018.
- This paper contains a more detailed description of learning different encoders and decoders than the journal paper above.